一、李雅普诺夫优化中二次漂移函数的推导

李雅普诺夫优化的核心是通过设计 “李雅普诺夫函数” 和 “漂移项”，保证系统状态收敛到稳定点。以下以线性时不变系统为例（非线性系统推导逻辑类似，仅动力学方程更复杂），推导二次漂移函数的形式。

1. 系统定义与假设

考虑连续时间线性系统（离散时间推导类似，仅用差分替代微分）：$$\dot{x}(t) = Ax(t) + Bu(t)$$ 其中：

-$$x(t) \in \mathbb{R}^n$$为系统状态向量，
-$$u(t) \in \mathbb{R}^m$$ 为控制输入，
-$$A \in \mathbb{R}^{n \times n}$$、$$B \in \mathbb{R}^{n \times m}$$为系统矩阵（已知，体现动力学特性）。

目标：设计控制输入 $$u(t)$$，使系统状态 $$x(t)$$ 收敛到原点（稳定点，即 $$x^* = 0$$。

2. 李雅普诺夫函数的构造

李雅普诺夫函数 $$V(x)$$ 需满足：

• 正定性：$$V(x) > 0$$ 对所有 $$x \neq 0$$ 成立，且 $$V(0) = 0$$；

• 径向无界性：当 $$|x| \to \infty$$ 时，$$V(x) \to \infty$$（保证全局收敛）。

最常用的二次型李雅普诺夫函数为：$$V(x) = x^T P x$$ 其中 $$P \in \mathbb{R}^{n \times n}$$ 是正定对称矩阵（$$P > 0$$），确保 $$V(x)$$ 满足正定

3. 二次漂移函数的推导

“漂移” 指李雅普诺夫函数随时间的变化率（连续时间为导数，离散时间为差分），用于衡量系统偏离稳定点的趋势。

（1）连续时间漂移

对 $$V(x)$$ 求时间导数：

​ $$\dot{V}(x) = \frac{d}{dt} (x^T P x) = \dot{x}^T P x + x^T P \dot{x}$$

代入系统动力学方程

​ $$\dot{x} = Ax + Bu：dot{V}(x) = (Ax + Bu)^T P x + x^T P (Ax + Bu)$$

展开并利用用矩阵转置性质$$(AB)^T = B^T A^T$$：

​ $$\dot{V}(x) = x^T A^T P x + u^T B^T P x + x^T P A x + x^T P B u$$

因 (P) 对称$$P^T = P$$，故

​ $$ x^T P A x = (x^T P A x)^T = x^T A^T P x$$

合并同类项：

​ $$\dot{V}(x) = 2x^T A^T P x + u^T B^T P x + x^T P B u$$

为使系统稳定，需设计 $$u(t)$$ 使 $$\dot{V}(x) < 0$$（负定性，保证 $$V(x)$$ 随时间减小，即状态向原点收敛。

若采用线性反馈控制 $$u = -Kx$$, $$K$$ 为反馈增益矩阵，代入得： $

​ $$\dot{V}(x) = x^T \left( A^T P + P A - P B K - K^T B^T P \right) x$$

令$$Q = -(A^T P + P A - P B K - K^T B^T P)$$ ，则：

​ $$\dot{V}(x) = -x^TQx$$ 其中 $$Q > 0$$（正定）

因此 $$\dot{V}(x)$$ 是负定二次型，即漂移函数为二次形式。

（2）离散时间漂移

若系统为离散时间（更贴近强化学习的时序特性）：

​ $$x_{t+1} = A x_t + B u_t$$

则漂移定义为相邻时刻李雅普诺夫函数的差分：

​ $$\Delta V(xt) = V(x{t+1}) - V(xt) = x{t+1}^T P x_{t+1} - x_t^T P x_t$$

代入 $$x_{t+1} = A x_t + B u_t$$：

​ $$\Delta V(x_t) = (A x_t + B u_t)^T P (A x_t + B u_t) - x_t^T P x_t$$

展开得：

​ $$\Delta V(x_t) = x_t^T A^T P A x_t + x_t^T A^T P B u_t + u_t^T B^T P A x_t + u_t^T B^T P B u_t - x_t^T P x_t$$

合并后可写成：

​ $$\Delta V(x_t) = x_t^T (A^T P A - P) x_t + 2 x_t^T A^T P B u_t + u_t^T B^T P B u_t$$

这仍是关于$$x_t$$和$$u_t$$的二次型函数，即二次漂移函数。

4. Conclusion

李雅普诺夫优化的二次漂移函数（连续时间的$$\dot{V}(x)$$ 或离散时间的$$\Delta V(x_t)$$本质是二次型误差度量，通过约束状态（及控制输入）的二次项，确保系统向稳定点收敛。

二、SAC 中 TD 目标损失函数的推导

SAC（Soft Actor-Critic）是基于最大熵强化学习的算法，其价值网络的损失函数通过 TD（Temporal Difference）目标定义，核心是最小化 “预测 Q 值” 与 “bootstrapped 目标 Q 值” 的偏差。

1. 问题定义（马尔可夫决策过程，MDP）

SAC 的优化对象是 MDP，定义为 $(\mathcal{S}, \mathcal{A}, r, p, \gamma)$：

-$$\mathcal{S}$$：状态空间，$\mathcal{A}$：动作空间，
-$$r(s,a) \in \mathbb{R}$$：状态 $s$ 下执行动作$a$ 的即时奖励，
-$$p(s'|s,a)$$：状态转移概率（从$$s$$ 到 $$s'$$ ），
-$$\gamma \in [0,1)$$：折扣因子（未来奖励的权重）。

目标：学习策略 $$\pi(a|s)$$（状态 $$s$$ 下动作 $$a$$ 的概率分布），最大化累积熵奖励：

​ $$J(\pi) = \mathbb{E}{\tau \sim \pi} \left[ \sum{t=0}^\infty \gamma^t \left( r(s_t,a_t) + \alpha H(\pi(\cdot|s_t)) \right) \right]$$

其中 $$H(\pi(\cdot|s)) = -\mathbb{E}_{a \sim \pi} [\log \pi(a|s)]$$ 是策略的熵（鼓励探索），$$\alpha > 0$$ 是熵温度参数。

2. 软 Q 值（Soft Q-Function）的定义

为量化策略的累积熵奖励，定义 “软 $$Q$$ 值” $$Q^\pi(s,a)$$ 为：
$$Q^\pi(s,a) = \mathbb{E} \left[ \sum{k=0}^\infty \gamma^k \left( r(s{t+k}, a{t+k}) + \alpha H(\pi(\cdot|s{t+k})) \right) \bigg| s_t = s, a_t = a \right]$$

利用时序分解（类似贝尔曼方程），软 Q 值满足：
$$Q^\pi(s,a) = r(s,a) + \gamma \mathbb{E}_{s' \sim p, a' \sim \pi} \left[ Q^\pi(s', a') \right]$$
（推导：将累积和拆分为即时奖励 + 未来奖励的折扣期望，因$$a' \sim \pi$$，故未来熵奖励已包含在$$Q^{\pi}(s',a')$$中）。

3. TD 目标与损失函数的构造

SAC 通过价值网络参数化软 $$Q$$ 值：$$Q_\theta(s,a) \approx Q^\pi(s,a)$$（$\theta$ 为网络参数）。为优化 $$\theta$$，需定义损失函数，使其最小化 “预测 $$Q$$ 值” 与 “目标 $$Q$$ 值” 的偏差。

（1）TD 目标的定义

目标 $$Q$$ 值（TD 目标）由 “即时奖励 + 未来软 $$Q$$ 值的折扣期望” 构成，为避免训练不稳定，SAC 使用目标网络 $$Q_{\theta'}$$（参数 $$\theta$$缓慢更新，与 $$\theta$$ 分离）：

​ $$y_t = rt + \gamma \mathbb{E}{a' \sim \pi\phi} \left[ Q{\theta'}(s', a') - \alpha \log \pi_\phi(a'|s') \right]$$

其中：

-$$\pi\phi(a|s)$$ 是参数化策略（$$\phi$$ 为策略参数），
-减去$$\alpha \log \pi\phi(a'|s')$$ 是因为：$$\mathbb{E}{a' \sim \pi} [Q^\pi(s',a')]=\mathbb{E}{a' \sim \pi}[Q_{\theta'}(s',a')-\alpha\log\pi(a'|s')]$$（软 Q 值的性质）。

（2）损失函数的推导

价值网络的优化目标是最小化 “预测 $$Q$$ 值$$Q_\theta(s,a)$$” 与 “TD 目标$$y_t$$” 的均方误差（MSE），即：

​ $$\mathcal{L}(\theta) = \mathbb{E}{(s,a,r,s') \sim \mathcal{D}} \left[ \left( Q\theta(s,a) - y_t \right)^2 \right]$$

其中$$\mathcal{D}$$是经验回放池（存储历史样本 $$(s,a,r,s')$$）。

代入$$y_t$$的表达式，损失函数展开为：

​ $$\mathcal{L}(\theta) = \mathbb{E} \left[ \left( Q\theta(s,a) - \left( r + \gamma \mathbb{E}{a' \sim \pi\phi} \left[ Q{\theta'}(s',a') - \alpha \log \pi_\phi(a'|s') \right] \right) \right)^2 \right]$$

4. 核心结论

SAC 的 TD 目标损失函数是二次型误差，衡量 “当前 $$Q$$ 值预测” 与 “基于未来奖励和策略熵的目标值” 的偏差，通过梯度下降最小化该误差，使 $$Q$$ 值估计收敛到真实软 $$Q$$ 值。

三、两者数学结构的相似性对比

通过推导可见，两个公式的核心相似性体现在二次型误差和时序递推的数学结构上：

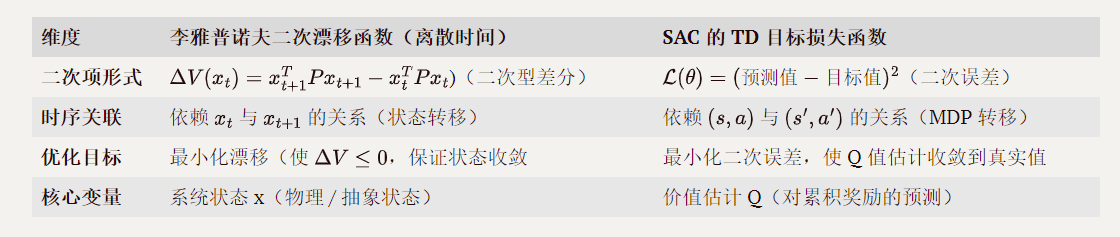
汇总

两者的数学推导均围绕 “二次型误差度量” 和 “相邻时间步的递推关系” 展开：李雅普诺夫漂移通过状态的二次型差分约束系统稳定性，SAC 的 TD 损失通过 Q 值的二次误差约束估计准确性。这种相似性源于动态系统优化的共性需求 — 用可微的二次项量化偏差，并通过时序关联将长期目标转化为局部优化问题。